Aperçu des semaines

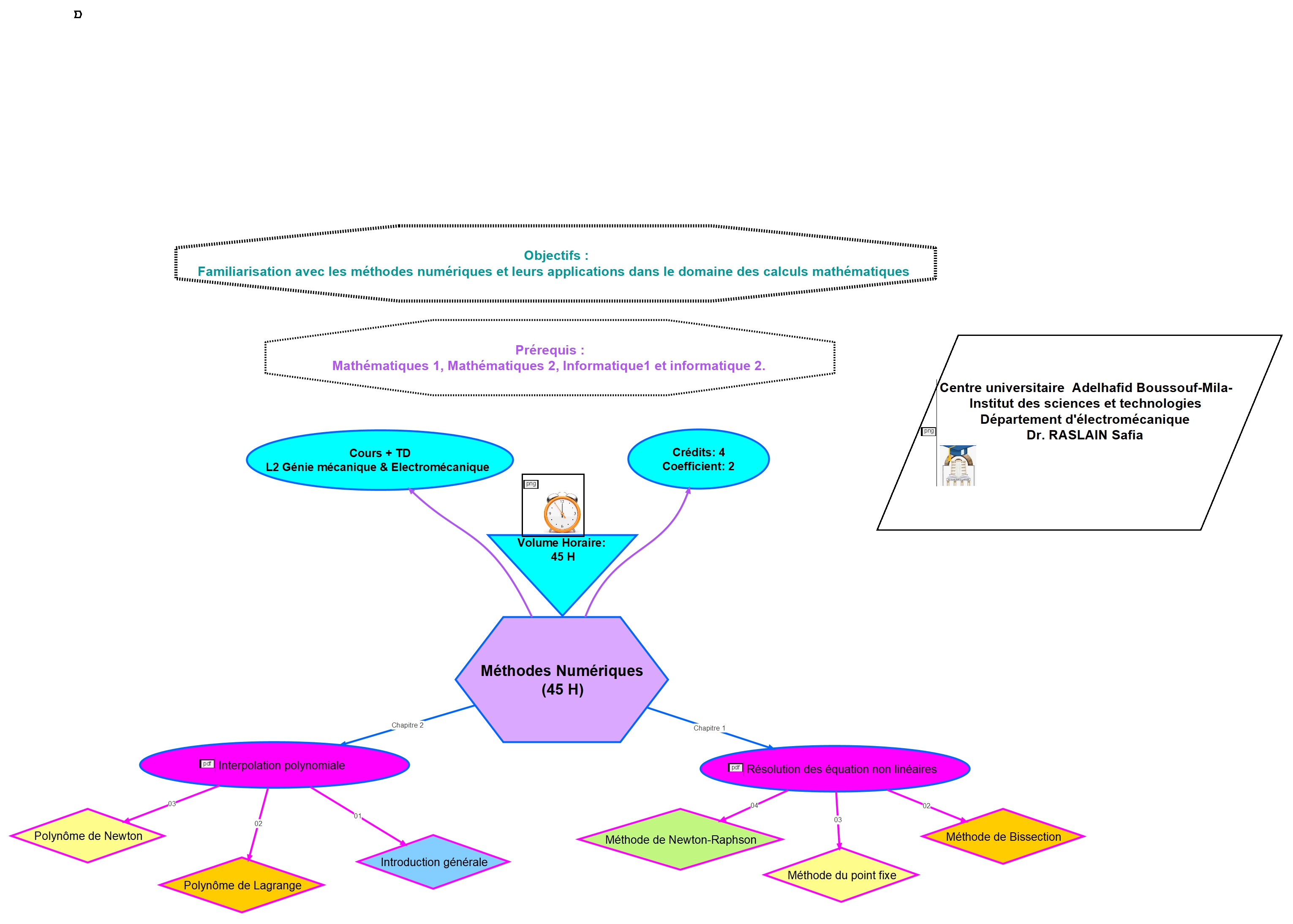
  • Cours Méthodes Numériques

    •  Le cours "Méthodes numériques" vise à fournir aux étudiants les outils nécessaires pour résoudre des problèmes mathématiques complexes à l'aide d'algorithmes numériques.
    • Ce module couvre des méthodes telles que la résolution numérique des équations non linéaires, l'interpolation, l'intégration numérique, et la résolution des systèmes d'équations linéaires                        

                     

  • La présentation de l'auteur

     Enseignant : Dr. Safia RASLAIN

    Contact par mail : s.raslain@centre-univ-mila.dz

    Etablissement : Centre universitaire Abd elhafid Boussouf Mila

    Institut : des Sciences et de Technologie

    Département : Electromécanique / Génie mécanique  

    Public cible : 2eme  année Licence.

    Disponibilité : Disponible au département le mardi de 13h00 à 16h00 et le jeudi de 08h00 à 12h30.

                                                                                    

    • Identification de la matière :

      Matière : Cours méthodes numériques

      Unité d’enseignement : UEF 2.2.2

      Horaire cours : Jeudi de 08h00 à 12h30

      Crédit : 04

      Coefficient : 02

      Volume horaire hebdomadaire total : 04h30


  • Objectifs du cours

    L’apprentissage visé par ce cours, dans son ensemble est que les étudiants devraient développer :

    En termes de savoir :

    •  Comprendre les concepts fondamentaux des méthodes numériques.
    • Appréhender les algorithmes utilisés pour la résolution de problèmes numériques.

    En termes de Savoir-faire :

    • Appliquer les techniques numériques pour résoudre des équations mathématiques complexes.
    • Analyser la performance des méthodes numériques et choisir les plus appropriées.

    En termes de Savoir-être :

    • Développer la rigueur scientifique et l'esprit critique dans l'application des méthodes numériques.
    •  Collaborer efficacement en équipe pour résoudre des problèmes numériques.

                                                                         

    • Prés-requis

      Il est recommandé aux apprenants de connaître :

      •  La connaissance de l'algèbre linéaire, des fonctions, des dérivées, et de l'intégration est essentielle.
      •  La maîtrise d'un langage de programmation (comme Python, MATLAB ou C++) est souvent requise pour implémenter les algorithmes numériques.
      •  La connaissance des notions préliminaires en analyse numérique, comme l'erreur numérique et la convergence, sont utiles pour comprendre les méthodes présentées.

                                                                              


    • Plan du cours

      • Introduction
      • Chapitre 1 : Méthodes de résolution des équations non linéaires.
      • Chapitre 2 : Interpolation polynomiale.
                                                             

    • Introduction

      Les méthodes numériques constituent un domaine des mathématiques appliquées qui se concentre sur le développement et l'application d'algorithmes pour résoudre des problèmes mathématiques complexes de manière approximative. Ces techniques sont essentielles lorsqu'une solution analytique exacte est impossible ou impraticable à obtenir. Les méthodes numériques englobent divers sujets, tels que la résolution d'équations différentielles, l'intégration et la dérivation numériques, la résolution de systèmes d'équations linéaires et non linéaires, ainsi que l'interpolation et l'approximation de fonctions. Elles sont largement utilisées dans les domaines de l'ingénierie, de la physique, de l'économie et d'autres disciplines scientifiques pour modéliser et simuler des phénomènes réels.

      La figure 1 présente la carte conceptuelle du cours

      • Chapitre 1 : Méthodes de résolution des équations non linéaires

      • Chapitre 2 : Interpolation polynomiale

      • Test de sortie

      • Bibliographie

        K. MEBARKI , Analyse Numérique, Cours, 2éme année licence mathématiques , Université Abderrahmane Mira de Béjaia.

        A. Boutayeb , M. Derouich , M. Lamlili et W. Boutayeb , Analyse Numérique : SMA-SMI S4.

        P. GOATIN , Analyse Numérique , Université du Sud Toulon-Var ISITV - 1ère année.

        Dr BOUSSOUFI Mustapha , Méthodes Numériques , Université des sciences et de technologie MOHAMED BOUDIAF D'oran - Conforme au programme de la 2eme année licence.

        G. Allaire et S.M. Kaber, Algèbre linéaire numérique, Ellipses, 2002. 

        P. G. Ciarlet, Introduction à l’analyse numérique matricielle et à l’optimisation,

            Masson, Paris, 1982.

        G. Allaire et S.M. Kaber, Introduction à Scilab. Exercices pratiques corrigés   d'algèbre linéaire, Ellipses, 2002.




        • 4 avril - 10 avril