-
Cacher les blocs
- Plein écran
- Vue standard
Aperçu des semaines
La présentation de l'auteur
Dr. CHELLOUF YASSAMINE
Centre Universitaire Abdelhafid Boussouf Mila
Faculté des sciences et technologie
Département de math
Email: y.chellouf@centre-univ-mila.dz
Objectifs de cours
- Connaître les notions des ensembles, les fonctions et domaine de définition, limites et continuité, dérivabilité, les intégrales.
- Définir les fonctions de deux variables et comprend comment trouver ses domaines de définition.
- Calculer les dérivées partielles première et deuxième ordre.
- Calculer les intégrales doubles.
- Connaître l'analyse combinatoire qui étudie comment de nombrer des objets.
- Évaluer les connaissance des apprenants.

Pré-requis
1. Quelle que notions sur les ensembles réels et sous-ensembles:
- Les entier naturels.
- Les entiers relatifs.
- Les décimaux.
- Les rationnels.
- Les réels.
2. Ordre et opérations algébrique.
3. Quelle que notions sur les fonctions numérique:
- Notions d'une fonction.
- Domaine de définition.
- Le graphe d'une fonction.
- Fonctions monotones.
- Fonctions réciproque.
- Les entier naturels.
Pré-test
1. Indiquer si les affirmations suivantes sont vraies ou fausses.
- Tout nombre réel est un nombre rationnel.
- 0,5 est un nombre rationnel.
- Le carré d'un nombre irrationnel n'est jamais rationnel.
- Il n'existe aucun nombre réel qui ne soit pas un nombre décimal.
- Le quotient de deux nombres décimaux non nuls est également un nombre décimal.
- L'inverse d'un nombre décimal peut être un nombre entier.
- Il existe deux nombres rationnels dont la somme est un nombre entier.
2. Déterminer le domaine de définition de la fonction f définie par: f(x)=3|x|+5.
3. Soit la fonction f définit par:
\( f:]-1,1[ \rightarrow \mathbb{R}\\ ~~~~~~~~~ x \rightarrow f(x)=\frac{x}{1-x^2} \) .
Montrer que f admet une fonction réciproque que l'on déterminera.- Tout nombre réel est un nombre rationnel.
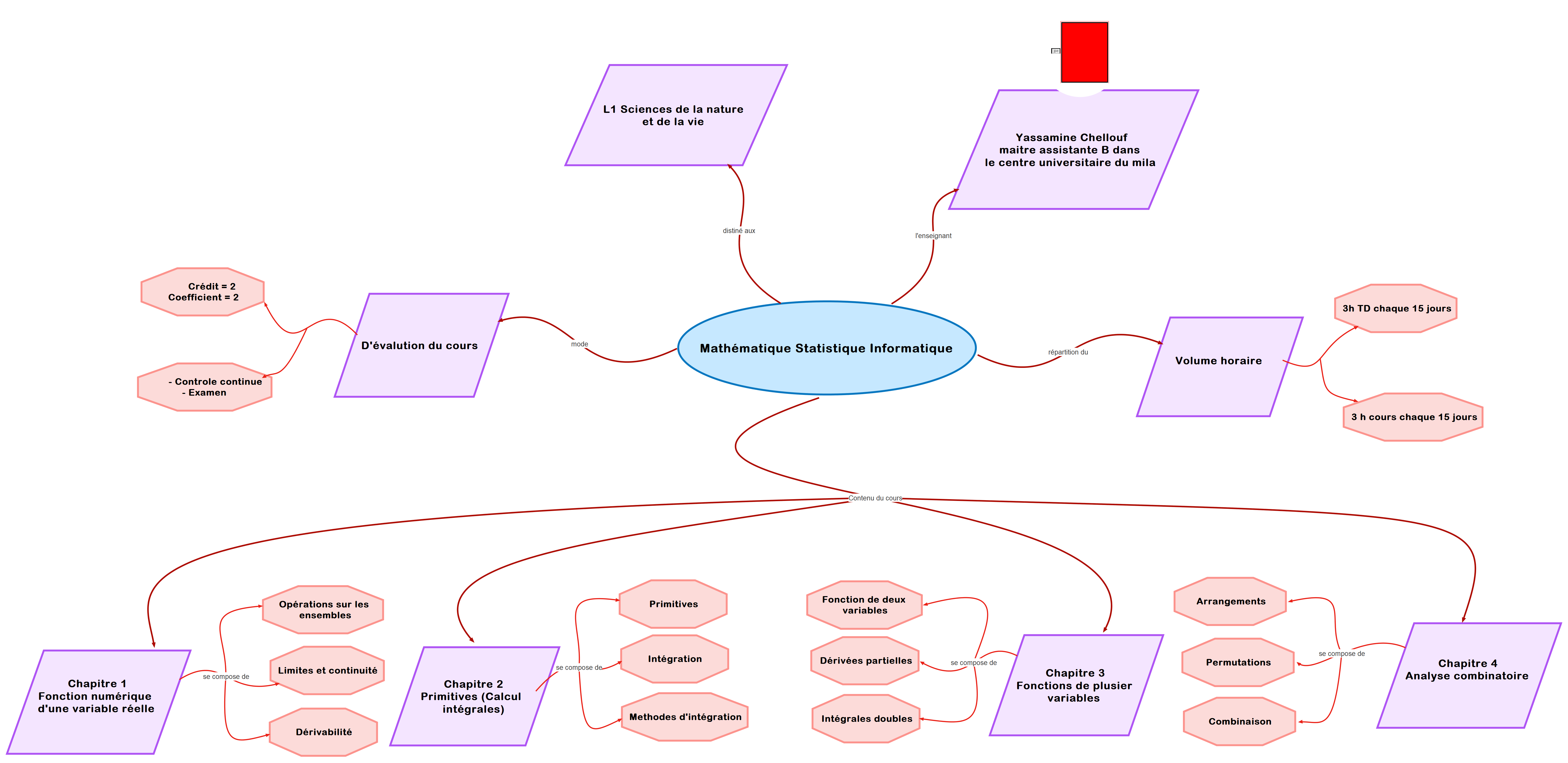
Plan global
1. Fonction numérique d'une variable réelle
2. Primitives (Calcul intégrales)
3. Fonctions de plusieur variables
4. Analyse combinatoire
Test de sortie
Exercice 1:
- Calculer les premières et les deuxième dérivées de \( f(x)=x\ln(\sqrt{x}) \).
- Calculer l'intégrale: \( \int_{1}^{e}f(x)~dx \).
Calculer les intégrales suivants a l'aide d’intégration par partie:- \( \int_{0}^{\frac{\pi}{2}}t\sin t ~dt \).
- \( \int_{0}^{\frac{\pi}{2}}t^2\sin t ~dt \).
Exercice 3:
1. Étudier la dérivabilité sur \( \mathbb{R} \) de la fonction f définie par:
\( f(x) =x\sin(x)\sin(\frac{1}{x}),~~si~~x\neq0~~et~~0~~si~~x=0 \).
2. Calculer l’intégrale suivant:
\( \int_{0}^{1}\frac{e^x}{\sqrt{e^x+1}}dx \).Exercice 4:
1. Étudier la continuité en (0,0) de la fonction f défini par:
\( f(x,y)=\frac{xy^2}{x^2+y^2}~~si~~(x,y)\neq(0,0),~~et~~0~~si~~(x,y)=(0,0) \).
2. Déterminer les dérivées partielles d’ordre 1 et 2 de la fonction g défini par:
\( g(x,y)=(x^2+y^2)(\cos x+\sin y),~\forall (x,y)\in \mathbb{R}^2 \).- Calculer les premières et les deuxième dérivées de \( f(x)=x\ln(\sqrt{x}) \).
Références
- Université Paris-Dauphine. DUMI2E, Algèbre 1, 2009-2010.
- Christian Houzel, « Limite (notion de) », Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis et Albin Michel, Paris 1997
- J.-F. Burnol, Continuité et dérivabilité en un point et fonction réciproque
- Jean-Yves Briend, Petit traité d'intégration, EDP Sciences, 2014, aperçu sur Google Livres
22 septembre - 28 septembre
x''(t) - 2x'(t) - 5x(t) = 0;
Donner toutes les solutions de cette equation
