Topic outline
Contact Form
Institute : Science and TechnologyDepartment: Common Core Department of Science and TechnologyTarget public: First Year Common Core of Science and Technology (LMD).Fields of Specialization: MathematicsCourse title: Analysis 2Credit: 6Coefficient: 3Duration: 15 weeksWeekly timetable: 1h 30 min of course and 3 hours for tutorial groupPlace of teaching: Lecture hallTeacher: Hocine RANDJIContact: randji.h@centre-univ-mila.dz Randji.Hocine@yahoo.comEvaluation methods: A final exam , short tests.Chapter 01: Properties of the set of real numbers R
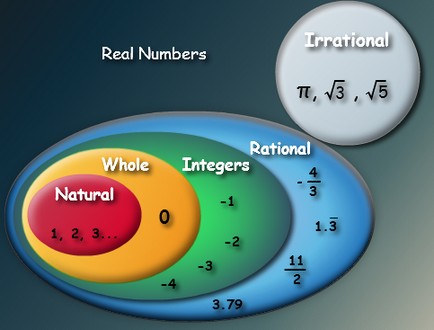
The main topics in this chapter are:
- Upper bound, lower bound, bounded set.
- Maximum element, minimum element.
- Supremum (least upper bound), infimum (greatest lower bound).
- Absolute value, integer part (floor function).
References:
:بالعربية.بابا حامد، بن حبيب، التحيل 1 تذكير بالدروس و تمارين محلولة عدد 300 ترجمة الحفيظ مقران، ديوان المطبوعات الجامعي *
In English
- Murray R. Spiegel, Schaum's outline of theory and problems of advanced calculus, Mcgraw-Hill (1968).
- Terence Tao, Analysis 1 (3rd edition), Springer (2016).
- Glyn James, Modern Engineering Mathematics, Pearson (2020).
- Bill Cox, Understanding Engineering Mathematics, Newnes, (2001).
En français:
- BOUHARIS Epouse, OUDJDI DAMERDJI Amel, Cours et exercices corrigés d’Analyse 1, Première année Licence MI Mathématiques et Informatique, U.S.T.O, 2020-2021.
- Benzine BENZINE, Analyse réelle cours et exercices corriges, première année maths et informatique (2016),
- N. Piskounov, Calcul differentiel et integral T1 (8ème édition), 2 édition mir. Moscou
