The heat diffusion equation

A major objective in a conduction analysis is to determine the temperature field in a medium resulting from conditions imposed on its boundaries. That is, we wish to know the temperature distribution, which represents how temperature varies with position in the medium.

Once this distribution is known, the conduction heat flux at any point in the medium or on its surface may be computed from Fourier’s law.

Note

Consider a homogeneous medium within which there is no bulk motion (advection) and the temperature distribution T(x, y, z) is expressed in Cartesian coordinates. The medium is assumed to be incompressible, that is, its density can be treated as constant. Following the four-step methodology of applying conservation of energy, we first define an infinitesimally small (differential) control volume, dx⋅dy⋅dz, as shown in Figure 3.

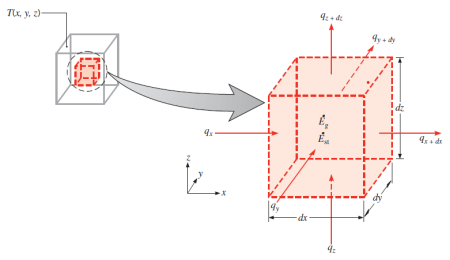
Figure 3 - Differential control volume, dx dy dz, for conduction analysis in Cartesian coordinates.

The express of conservation of energy using the foregoing rate equations. On a rate basis, the general form of the conservation of energy requirement is

E i ˙ + E g ˙ − E out ˙ = E st ˙ dot E_{i} + dot E_{g}- dot E_{out} = dot E_{st}

The general form, in Cartesian coordinates, of the heat diffusion equation.

∂ ∂ x ( k ∂ T ∂ x ) + ∂ ∂ y ( k ∂ T ∂ y ) + ∂ ∂ z ( k ∂ T ∂ z ) + q ˙ = ρ . c p . ∂ T ∂ t frac { partial } { partial x} (k frac { partial T} { partial x} ) + frac { partial } { partial y} (k frac { partial T} { partial y} ) + frac { partial } { partial z} (k frac { partial T} { partial z} ) + dot q = ρ. c_{p} . frac { partial T} { partial t}

This equation, often referred to as the heat equation, provides the basic tool for heat conduction analysis. From its solution, we can obtain the temperature distribution T(x, y, z) as a function of time.

Advice

It is often possible to work with simplified versions. For example, if the thermal conductivity is constant, the heat equation is

( ∂ ² T ∂ x ² ) + ( ∂ ² T ∂ y ² ) + ( ∂ ² T ∂ z ² ) + q ˙ k = 1 α ∂ T ∂ t (frac { partial²T } { partial x²})+(frac { partial²T } { partial y²})+(frac { partial²T } { partial z²})+ frac { dot q } {k} = frac {1} {α} frac { partial T} { partial t}

where

α = k ρ c p α = frac {k} {ρ c_{p} }

the thermal diffusivity

Note

Additional simplifications of the general form of the heat equation are often possible. For example, under steady-state conditions, there can be no change in the amount of energy storage; hence equation reduces to

∂ ∂ x ( k ∂ T ∂ x ) + ∂ ∂ y ( k ∂ T ∂ y ) + ∂ ∂ z ( k ∂ T ∂ z ) + q ˙ = 0 frac { partial } { partial x} (k frac { partial T} { partial x} ) + frac { partial } { partial y} (k frac { partial T} { partial y} ) + frac { partial } { partial z} (k frac { partial T} { partial z} ) + dot q = 0

Moreover, if the heat transfer is one-dimensional (e.g., in the x-direction) and there is no energy generation, equation reduces to

∂ ∂ x ( k ∂ T ∂ x ) = 0 frac { partial } { partial x} (k frac { partial T} { partial x} ) = 0

Fundamental

The important implication of this result is that, under steady-state, one-dimensional conditions with no energy generation, the heat flux is a constant in the direction of transfer

d q x ¨ dx = 0 {d ddot q_{x} } over {dx} =0