تعريفه:

نقول عن تجربة أنها "برنولية"[1] إذا كانت تحتمل نتيجتين (حدثين) متنافيتين A وB،نسمي A نجاح وB فشل.

نعتبر المتغير X الذي يمثل عدد مرات النجاح، يأخذ X القيمة 1 عند تحقق الحدث A والقيمة 0 في الحالة المعاكسة.

نرمز بـ p احتمال النجاح لاحتمال تحقق الحدث A وq=1-p احتمال الحدث المعاكس (الفشل)،[1][3][2][3]يعين توزيع برنولي كما يلي:

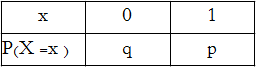
ونكتب:( X~B(1 ,𝑝[4]

حيث:

وp+q =1 ،أي حالة تجربة ثنائية مكررة n=1 مرة

والقانون الاحتمالي لهذا التوزيع هو:

p x = p ( X = x ) = { p x q 1 − x si x = 0,1 ; p + q = 1 0 si non } p_{x}=p( X=x )= lbrace binom{ p^{x} q^{1-x} si x= 0,1 ;p+q = 1}{0 si non} rbrace