Torseur de cohésion ou efforts de cohésion (efforts intérieurs)
Définition
On appelle force intérieure tout effort se trouvant entre les particules d’un corps. Ces forces tendent à s’opposer aux éventuelles déformations du corps dues aux forces extérieures. En résistance des matériaux, les forces intérieures qui apparaissent suite à l’application de forces extérieures s’appellent efforts internes. On distingue les efforts internes suivants :
• Effort normal (N) : c’est la somme algébrique des projections sur la normale de la section de toutes les forces extérieures situées d’un même côté de la section considérée.
• Effort tranchant (T) : c’est la somme géométrique des projections, sur le plan de la section de toutes les forces extérieures situées d’un même côté de la section.
• Moment de torsion (Mt) : c’est la somme géométrique des moments par rapport à la normale à la section au centre de gravité de toutes les forces extérieures situées d’un même côté.
• Moment de flexion (Mf) : c’est la somme géométrique des projections, sur le plan de la section, des moments pris par rapport au centre de gravité des forces extérieures situées d’un même côté de la section
Considérons une poutre en équilibre sous l’effet d’efforts extérieurs.
Effectuons virtuellement une coupure dans cette poutre et analysons l’équilibre des deux tronçons obtenus.
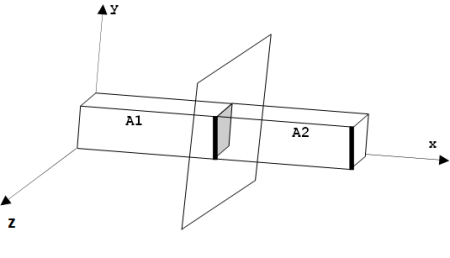
Les tançons A1 et A2 exerçaient l’un sur l’autre des actions qui maintenaient la cohésion entre les deux parties. Ces actions peuvent être représentées par un torseur appelé torseur des efforts intérieurs ou torseur de cohésion
Composition du torseur de cohésion
La liaison entre le tronçon A1 et A2 est supposée parfaite elle est donc modélisé par un encastrement. Le torseur de cohésion prend alors la forme la plus générale:
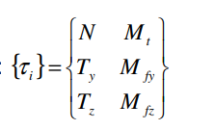
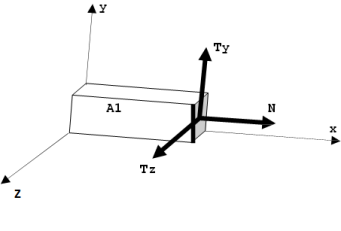
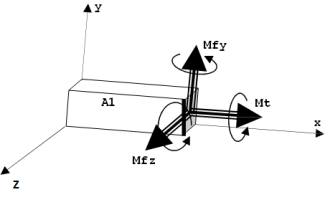
Avec :
N, effort normal : force de direction tangente à la courbe moyenne ;
T, effort tranchant : force perpendiculaire à la courbe moyenne et provoquant un cisaillaient:
o Ty : effort tranchant selon y,
o Tz : effort tranchant selon z ;
Mf, moment fléchissant : moment dont le vecteur est perpendiculaire à la courbe moyenne et provoquant une flexion :
o Mfy : moment fléchissant selon y,
o Mfz : moment fléchissant selon z ;
Mt, moment de torsion : son vecteur a pour direction x.
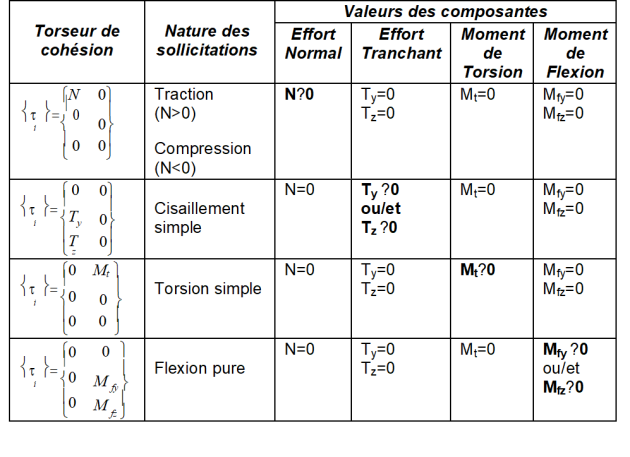
Cas particuliers du torseur de cohésion
Diagrammes
Le torseur de cohésion est modifié lorsque la coupure se déplace le long de la poutre. On étudie alors plusieurs coupures en particulier lorsqu’on rencontre : une discontinuité d’ordre géométrique (changement de direction de la ligne moyenne) ou une discontinuité liée à des efforts concentrés ou à une liaison. Le tracé des différentes valeurs prises par une composante du torseur de cohésion le long de la lige moyenne de la poutre en fonction de la position de la coupure est appelé diagramme. Le tracé des diagrammes permet de localiser les sections les plus sollicitées de la poutre et par conséquent de dimensionner la poutre pour résister aux efforts extérieurs, c’est l’un des objectifs de la RDM[1].