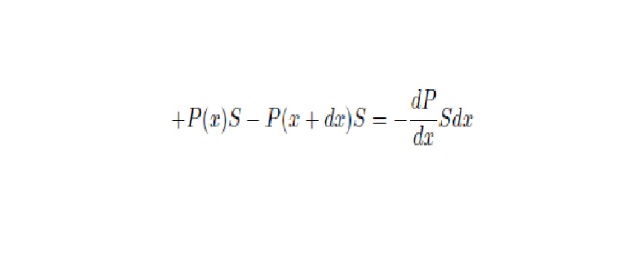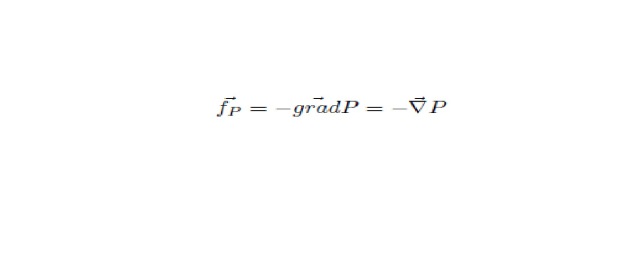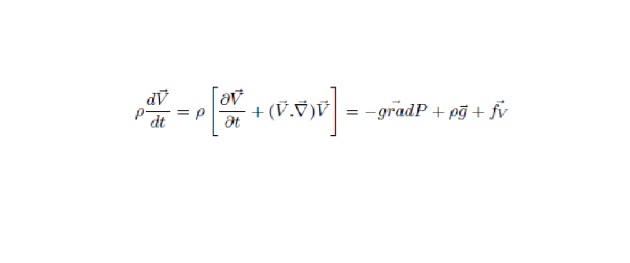Equation d'Euler
La relation de la Dynamique permettrait d'´étudier le mouvement de chaque particule fluide une `a une mais le nombre d'´équations à résoudre sera aussi
grand que le nombre de particules contenues dans le fluide. On réalise donc une approche dite de milieu continu dans laquelle on va exprimer la vitesse et
l'accélération du fluide en un point donné de écoulement (de coordonnées r et ceci en fonction du temps t). On cherche donc à établir une équation qui fournisse les valeur de la vitesse V (r, t) et de la pression P(r, t), ainsi que T (r, t), si le fluide n'est pas isotherme ou C (r, t) si le fluide transporte un constituant en solution de
concentration C. Pour cela on considère donc un élément de volume sur lequel on va d'abord exprimer la résultante des forces de pression (cf.
Figure 2. Pour une surface S et dans la seule direction x la force résultante (en
Newton) vaut :
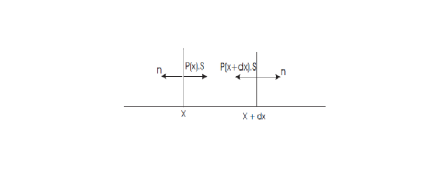
soit en divisant par le volume fluide S.dx la force volumique selon Ox se résume à – dP/dx . En généralisant aux 3 directions de l'espace on déduit la force résultante de pression :
L'équation d'Euler d'un fluide parfait soumis à des forces de pression, à la gravité et à d'éventuelles forces externes fV s'écrit :
Remarque :
1) Écoulement permanent : la dérivée par rapport au temps vaut 0 , cad. que la vitesse en un point quelconque ne varie pas avec le temps soit ∂V/∂t = 0.
2) Écoulement établi : signifie que l'écoulement cesse de varier en espace. Lorsqu'un fluide pénètre dans un tuyau par exemple, il faut une certaine longueur
(de l'ordre de 30 `a 50 fois le diamètre hydraulique) pour que le profil de vitesse ne varie plus suivant la direction d'avancement du fluide : on dit que l'´écoulement est alors établi d'où : ∂V/∂x = 0.
3) L'équation vectorielle d'Euler peut être projetée sur les 3 directions de l'espace et fournit ainsi 3 équations. Toutefois, un problème standard 3D de Mécanique des Fluides possède 4 inconnues : 3 de vitesse et 1 de pression : il manque donc une équation que nous allons voir maintenant.