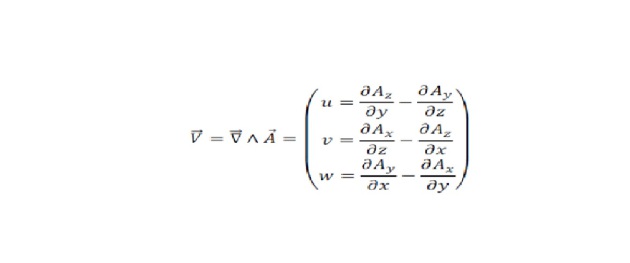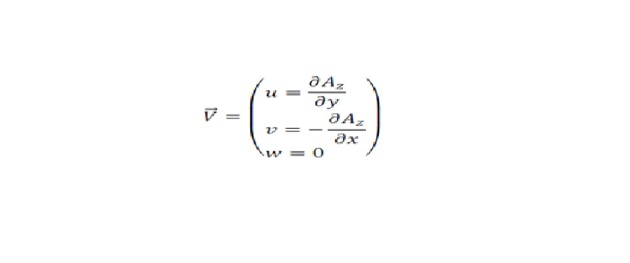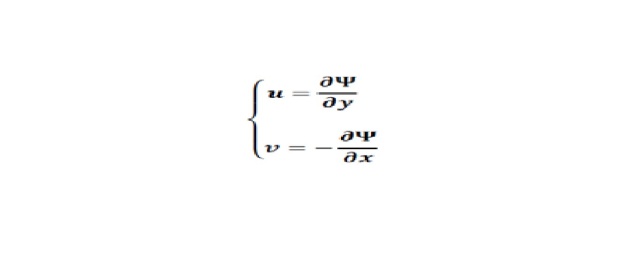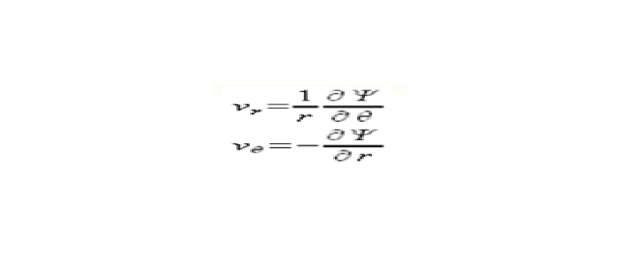Mécanique des fluides

Considérons l'écoulement conservatif d'un fluide incompressible. Dans ce cas,l'équation de continuité se formule simplement par : . Par ailleurs, quelle que soit la

quantité vectorielle , en tout point de l'espace la relation mathématique doit être vérifiée. Donc, par identification, on peut définir en tout point de l'espace le vecteur vitesse comme résultant de , où peut alors être qualifié de « potentiel vecteur ». La connaissance de ce potentiel vecteur en tout point de l'espace permet donc d'en déduire les trois composantes du vecteur vitesse en ce même point :

Considérons maintenant que l'écoulement est bidimensionnel, dans le plan (x,y), impliquant que w=0 et qu'il y ait invariance par translation suivant z, d'où . Il reste alors :

Dans ces conditions, on note que chaque vecteur vitesse est défini au moyen de seulement deux composantes et que celles-ci dérivent d'une seule composante

parmi les trois du potentiel vecteur. On peut donc en conclure que le champ de vecteurs vitesse d'un écoulement plan dérive d'une quantité scalaire, la fonction de courant . La connaissance de cette seule fonction de courant permet alors d'en déduire le champ de vecteurs vitesse en tout point de l'écoulement, par simple

application de :