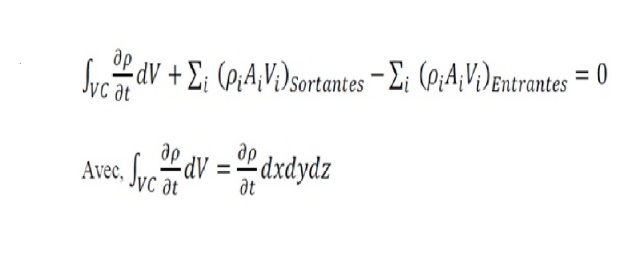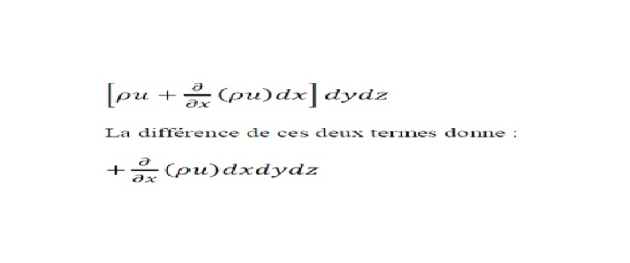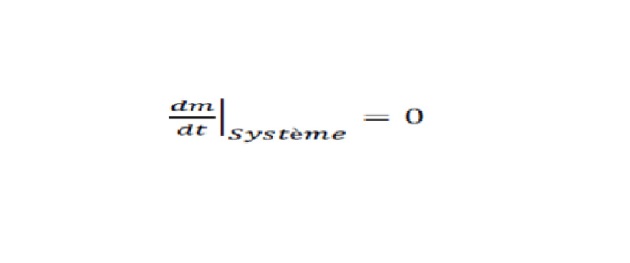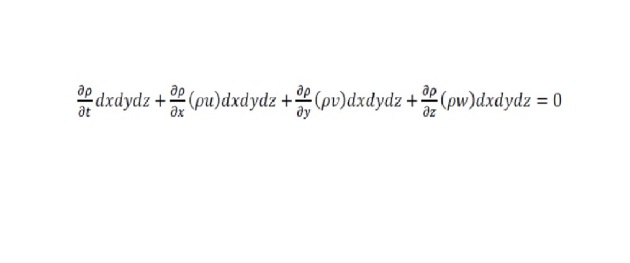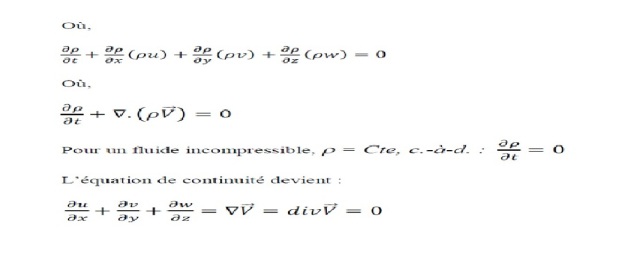L'équation de continuité
Définition :
Mathématiquement, elle est représentée, comme étant le taux de variation de masse d'un système est nul. Par définition, un système = quantité de masse fixe.
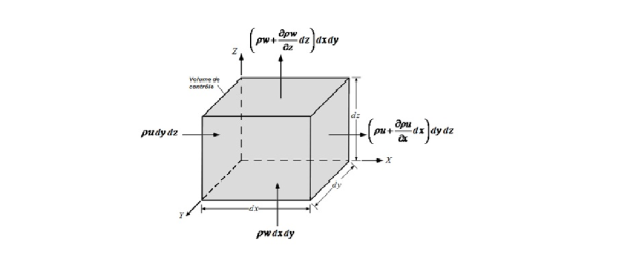
Considérons un élément fluide parallélépipédique de volume dV=dxdydz (voir Fig.I-5) incompressible au repos.
Essayons de développer les termes de l'équation ci-dessus suivant les trois axes ox, oy et oz. Pendant le temps dt, il entre par la face dydz un débit massique de fluide égale à :
ρudydz. Cinématique des fluides 15 Pendant le même temps, il sort part la face opposée dydz, un flux massique de fluide égale à celui qui est entré, augmenté de sa différentielle partielle par rapport à x. or seules les grandeurs u et ρ peuvent varier suivant x. le débit massique sortant est donc :
Qui représente la variation (augmentation) du débit massique traversant le parallélépipède. Par un raisonnement similaire, on peut déterminer la variation en débit à travers les autres faces. Les résultats obtenus sont regroupés dans le tableau I.1.
Après substitution de ces termes dans l'équation
on obtient :
C'est la forme recherchée de l'équation de conservation de masse pour un volume de contrôle infinitésimal dans un système de coordonnées cartésiennes.